The ideas in this write-up were originally explored in the context of the university course "Introduction to Computational Logic" by Prof. Gert Smolka and posted in the course-internal forum. Here, I want to elaborate on the forum post and give enough context to keep it mostly self-contained.
Kaminski's Equation
In the lecture, we learned about Kaminski's equation, an interesting statement about functions on boolean values ($\mathbb{B}$). It formally states the following.
$$ \Large \forall f : \mathbb{B}\to\mathbb{B}.\ \forall x.\ f\,(f\,(f\,x)) = f\,x $$
The equation was first introduced by Mark Kaminski, one of Smolka's former students, in his Bachelor's thesis on classical higher-order logic in 2005.
To understand why this is true, we first realize that $\mathbb{B}\to\mathbb{B}$ only contains 4 different functions. Since there are only two different input values, we can fully describe any function $f:\mathbb{B}\to\mathbb{B}$ by considering the values of $f\,0$ and $f\,1$. For each of those two values, we again only have two options, meaning there are $2^2$ functions in total.
In particular, those functions are $I$ (identity), $T$ (transpose/negation), $0$ (constant zero), and $1$ (constant one). For any $x:\mathbb{B}$, the identity ($I$) gives us $f\,x = x$, transpose ($T$) satisfies $f\,(f\,x) = x$, and the two constant functions ($0$, $1$) yield $f\,(f\,x) = f\,x$.
So $f\,(f\,(f\,x)) = f\,x$ is the shortest equation that is implied by all the above identities and therefore holds for all (four) functions $f:\mathbb{B}\to\mathbb{B}$ and all (two) values $x:\mathbb{B}$.
The General Case
You might have noticed that no part of Kaminski's equation is specific to "truth values". The same statement can be shown for any type that has exactly two elements. So we might start wondering if there is an analogous equation for types with three or four elements, or types with any fixed number of elements.
To make this idea more formal, we will define the generalized Kaminski equation using the following predicate.
$$ \Large G\,(n\,a\,b : \mathbb{N})\ :=\ \forall f : \mathbb{F}_n\to\mathbb{F}_n.\ \forall x : \mathbb{F}_n.\ f^a\,x = f^b\,x $$
Here, $\mathbb{F}_n$ refers to the finite type with $n$ elements (equivalent to $\{0, 1, 2, \dots, n-1\}$), and $f^n$ denotes repeated function application. Using this predicate, Kaminski's equation as discussed above may be expressed as $G\,2\,3\,1$, since $\mathbb{B}$ is equivalent to $\mathbb{F}_2 = \{0, 1\}$.
Initial Exploration
Let's get some intuition for how this predicate $G$ behaves. Since both $f$ and $x$ are finite, we can compute the predicate for any choice of $n$, $a$, and $b$ by brute force. This isn't very efficient since $\mathbb{F}_n$ has $n$ elements and $\mathbb{F}_n\to\mathbb{F}_n$ has $n^n$ elements, but it's doable for small values of $n$.
Here are visualizations for $G\,3$ and $G\,4$.
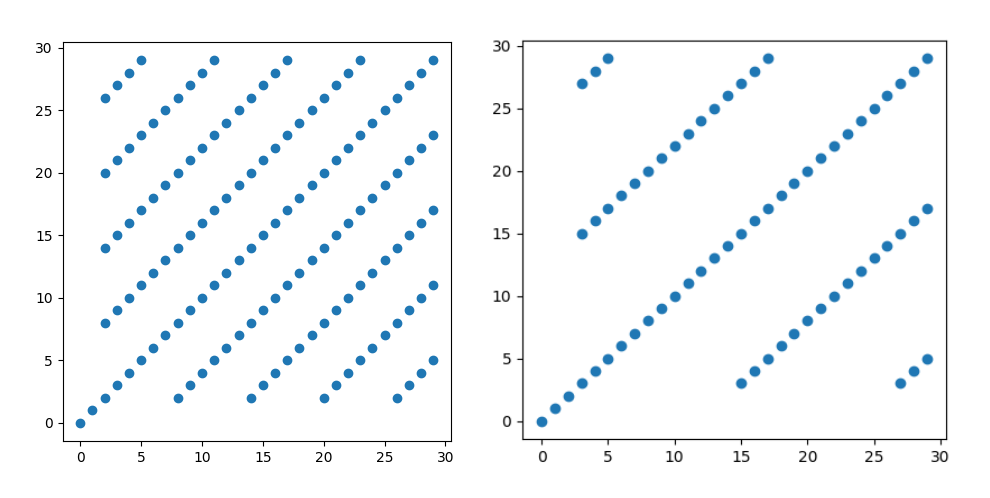
Basic Properties
There is already some interesting structure to unpack in the two plots above. Let's try to explain what's going on here.
First, $G\,n$ is an equality relation. This follows directly from the equality used in the definition of $G$. The reflexivity property ($G\,n\,a\,a$) explains the middle diagonal and the symmetry property ($G\,n\,a\,b\leftrightarrow G\,n\,b\,a$) explains the symmetry axis in both plots.
Next, we notice that $G\,n$ is additive, i.e. $G\,n\,a\,b \to G\,n\,c\,d \to G\,n\,(a+c)\,(b+d)$. This is true, since $f^{a+c}\,x = f^{b+d}\,x$ can be rewritten as $f^a\,(f^c\,x) = f^b\,(f^d\,x)$. Now the second assumption ($G\,n\,c\,d$) tells us that $f^c\,x = f^d\,x = y$, so it suffices to show $f^a\,y = f^b\,y$, which is given by the first assumption ($G\,n\,a\,b$).
Using additivity and reflexivity, we get $G\,n\,a\,b \to G\,n\,(a+c)\,(b+c)$, which explains why all solutions trail off towards infinity in the plots. We will refer to this as the "trailing" property.
Next, we have $G\,n\,a\,(a+b) \to G\,n\,a\,(a+b+b)$. By applying the assumption twice, we get $f^a\,x = f^{a + b}\,x = f^b\,(f^a\,x) = f^b\,(f^{a + b}\,x) = f^{a + b + b}\,x$, which is what we wanted to show. This explains why the solutions seem to repeat at a fixed interval going away from the middle diagonal. We will refer to this as the "extra lap" property.
At this point, we understand almost all the complexity we see in the plots. Once we know the smallest non-trivial solution to $G\,n$, so the first solution that is not on the middle diagonal, we can use the above properties to unfold the entire plot.
Non-Trivial Solutions
We want to show that $G\,n$ has non-trivial solutions, i.e. $\exists a b.\ a\neq b\wedge G\,n\,a\,b$. Consider the function $g\,(k : \mathbb{N})\,(f : \mathbb{F}_n\to\mathbb{F}_n)\,(x : \mathbb{F}_n) := f^k\,x$. Since $g$ takes an infinite type as its first argument and returns a finite type, it cannot be injective. Formally, that is to say $\neg\forall ab.\ g\,a = g\,b\to a = b$. By expanding $g$, we get $\neg\forall ab.\ (\forall f x.\ f^a\,x = f^b\,x)\to a = b$. Finally, we push the negation to get $\exists ab.\ (\forall f x.\ f^a\,x = f^b\,x)\wedge a \neq b$, which is what we wanted to show.
So now we know that every $G\,n$ has non-trivial solutions, we only need to figure out where they are. We can once again use brute force to find the first couple of these solutions.
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | ... |
|---|---|---|---|---|---|---|---|
| $a$ | 0 | 1 | 2 | 3 | 4 | 5 | ... |
| $b$ | 1 | 3 | 8 | 15 | 64 | 65 | ... |
The sequence for $a$ is fairly straightforward. For $b$, I had to consult the OEIS, which only gave me a single match (A065500) for the above sequence.
This leads us to conjecture the following statement.
$$ \Large \forall n.\ G\,n\,(n-1)\,(\operatorname{lcm}(1\dots n)+n-1) $$
Here, the $\operatorname{lcm}(1\dots n)$ is the least common multiple of all natural numbers from $1$ to $n$. It is the smallest natural number that is divisible by all natural numbers from $1$ to $n$.
The proof for $G\,3\,2\,8$
Before we prove the full statement, we will walk through the proof of $G\,3\,2\,8$. That is, we want to show the following.
$$ \Large \forall f : \mathbb{F}_3\to\mathbb{F}_3.\ \forall x : \mathbb{F}_3.\ f^2\,x = f^8\,x $$
Here, we have two cases to consider.
Case $f$ is not surjective.
In this case, there must be at least one element in $\mathbb{F}_3$ that is not in the image of $f$. This means the image of $f$ can be fully described by $\mathbb{F}_2$, so we only have to show $G\,2\,1\,7$.
Using the "extra lap" property twice, we can rewrite $G\,2\,1\,(1+2+2+2)$ to $G\,2\,1\,(1+2)$. Finally, we need to show $G\,2\,1\,3$, which is Kaminski's original equation.
(You can imagine that the proof for $G\,4\,3\,15$ is going to fall back to this proof here).
Case $f$ is surjective.
Since the function $f$ is surjective and has exactly $n$ different values as input and output, there must be exactly one input for every output, so $f$ is also injective. This means $f$ must be a bijection, and hence a permutation.
The cycle length of this permutation could be $1$, $2$, or $3$. In general, it's not possible to have cycles in $\mathbb{F}_n$ that are longer than $n$. This is because, if you make a list of the values $f^0 x$, $f^1 x$, $f^2 x$ to $f^n x$, then there are $n+1$ elements, but at most $n$ of those can be distinct.
If we apply $f$ to some value $6$ times, we are guaranteed to get the original value back, since $6$ is a multiple of all possible cycle lengths.
This means we get $G\,3\,0\,6$ for this case. Using the "trailing" property, we get $G\,3\,2\,8$, which is what we wanted to show.
Finally, we want to prove the general case.
The Proof for the General Case
$$ \Large \forall n.\ G\,n\,(n-1)\,(\operatorname{lcm}(1\dots n)+n-1) $$
Proof by natural induction over $n:\mathbb{N}$.
Case $n = 0$.
Since $\mathbb{F}_0$ is empty, this case is trivial.
Case $n \to n + 1$.
We need to show $G\,(n+1)\,n\,(\operatorname{lcm}(1\dots (n+1))+n)$.
Here, we have two cases to consider.
Case $f$ is not surjective.
Here, the image of $f$ can be fully described by $\mathbb{F}_n$.
So it suffices to show $G\,n\,(n-1)\,(\operatorname{lcm}(1\dots (n+1))+n-1)$.
Let $k$ be $\operatorname{lcm}(1\dots (n+1))\,/\,\operatorname{lcm}(1\dots n)$.
Using "extra lap" $k$-times, we get $G\,n\,(n-1)\,(\operatorname{lcm}(1\dots n)+n-1)$, which is the inductive hypothesis.
Case $f$ is surjective.
Now we know $f$ is a permutation with cycle length $\le n+1$.
So $f^{\operatorname{lcm}(1\dots (n+1))}$ is identity, since $\operatorname{lcm}(1\dots (n+1))$ is a multiple of the cycle length by construction.
This gives us $G\,(n+1)\,0\,(\operatorname{lcm}(1\dots (n+1)))$ for this case.
Using the "trailing" property, we get $G\,(n+1)\,n\,(\operatorname{lcm}(1\dots (n+1))+n)$, which is what we wanted to show.
Qed.
Conclusion
We have proven the Generalized Kaminski Equation:
$$ \Large \forall n.\ \forall f : \mathbb{F}_n\to\mathbb{F}_n.\ \forall x.\ f^{n-1}\,x = f^{\operatorname{lcm}(1\dots n) + n - 1}\,x $$
After posting my results to the course-internal forum, I was handed one (1) cookie as a reward for my efforts1 (it was worth it).
Is this equation useful? Probably not. The $\operatorname{lcm}(1\dots n)$ grows exponentially. If you have some unknown function on 4-bit numbers (so $\mathbb{F}_{16}$), you need $720\,735$ application of that function until you can safely replace it with just $15$ applications. For 5-bit numbers, you already need $144\,403\,552\,893\,631$ iterations before you can simplify anything.
Anyway, that's it, thank you.
Prof. Smolka also approached me about the post a few days later and offered to supervise my bachelor's thesis. Unfortunately, I was already working on my thesis with another professor then and had to turn down the offer. ↩︎